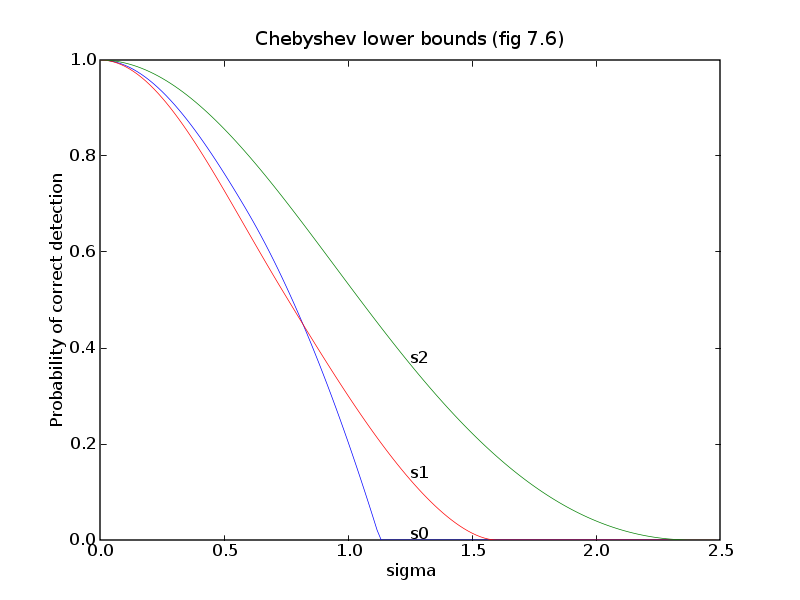
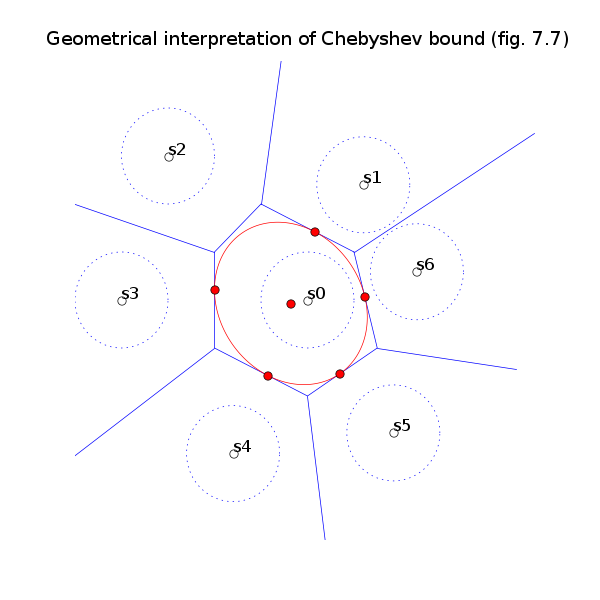
# Figures 7.6 and 7.7, page 383.
# Chebyshev bounds.
from math import pi, sqrt
from cvxopt import matrix, spmatrix, mul, cos, sin, solvers, blas, lapack
solvers.options['show_progress'] = False
try: import pylab
except ImportError: pylab_installed = False
else: pylab_installed = True
# Extreme points and inequality description of Voronoi region around
# first symbol (0,0).
m = 6
V = matrix([ 1.0, 1.0,
-1.0, 2.0,
-2.0, 1.0,
-2.0, -1.0,
0.0, -2.0,
1.5, -1.0,
1.0, 1.0 ], (2,m+1))
A0 = matrix([-(V[1,:m] - V[1,1:]), V[0,:m] - V[0,1:]]).T
b0 = mul(A0, V[:,:m].T) * matrix(1.0, (2,1))
# List of symbols.
C = [ matrix(0.0, (2,1)) ] + \
[ 2.0 * b0[k] / blas.nrm2(A0[k,:])**2 * A0[k,:].T for k in range(m) ]
# Voronoi set around C[1]
A1, b1 = matrix(0.0, (3,2)), matrix(0.0, (3,1))
A1[0,:] = -A0[0,:]
b1[0] = -b0[0]
A1[1,:] = (C[m] - C[1]).T
b1[1] = 0.5 * A1[1,:] * ( C[m] + C[1] )
A1[2,:] = (C[2] - C[1]).T
b1[2] = 0.5 * A1[2,:] * ( C[2] + C[1] )
# Voronoi set around C[2]
A2, b2 = matrix(0.0, (3,2)), matrix(0.0, (3,1))
A2[0,:] = -A0[1,:]
b2[0] = -b0[1]
A2[1,:] = (C[1] - C[2]).T
b2[1] = 0.5 * A2[1,:] * ( C[1] + C[2] )
A2[2,:] = (C[3] - C[2]).T
b2[2] = 0.5 * A2[2,:] * ( C[3] + C[2] )
def cheb(A, b, Sigma):
# Calculates Chebyshev lower bound on Prob(A*x <= b) where
# x in R^2 has mean zero and covariance Sigma.
#
# maximize 1 - tr(Sigma*P) - r
# subject to [ P, q - (tauk/2)*ak ]
# [ (q - (tauk/2)*ak)', r - 1 + tauk*bk ] >= 0,
# k = 0,...,m-1
# [ P, q ]
# [ q', r ] >= 0
# tauk >= 0, k=0,...,m-1.
#
# variables P[0,0], P[1,0], P[1,1], q[0], q[1], r, tau[0], ...,
# tau[m-1].
m = A.size[0]
novars = 3 + 2 + 1 + m
# Cost function.
c = matrix(0.0, (novars,1))
c[0], c[1], c[2] = Sigma[0,0], 2*Sigma[1,0], Sigma[1,1]
c[5] = 1.0
Gs = [ spmatrix([],[],[], (9,novars)) for k in range(m+1) ]
# Coefficients of P, q, r in LMI constraints.
for k in range(m+1):
Gs[k][0,0] = -1.0 # P[0,0]
Gs[k][1,1] = -1.0 # P[1,0]
Gs[k][4,2] = -1.0 # P[1,1]
Gs[k][2,3] = -1.0 # q[0]
Gs[k][5,4] = -1.0 # q[1]
Gs[k][8,5] = -1.0 # r
# Coefficients of tau.
for k in range(m):
Gs[k][2, 6+k] = 0.5 * A[k,0]
Gs[k][5, 6+k] = 0.5 * A[k,1]
Gs[k][8, 6+k] = -b[k]
hs = [ matrix(8*[0.0] + [-1.0], (3,3)) for k in range(m) ] + \
[ matrix(0.0, (3,3)) ]
# Constraints tau >= 0.
Gl, hl = spmatrix(-1.0, range(m), range(6,6+m)), matrix(0.0, (m,1))
sol = solvers.sdp(c, Gl, hl, Gs, hs)
P = matrix(sol['x'][[0,1,1,2]], (2,2))
q = matrix(sol['x'][[3,4]], (2,1))
r = sol['x'][5]
bound = 1.0 - Sigma[0]*P[0] - 2*Sigma[1]*P[1] - Sigma[3]*P[3] - r
# Worst-case distribution from dual solution.
X = [ Z[2,:2].T / Z[2,2] for Z in sol['zs'] if Z[2,2] > 1e-5 ]
return bound, P, q, r, X
# Compute bound for s0 with sigma = 1.0.
# Write ellipse {x | x'*P*x + 2*q'*x + r = 1} in the form
# {xc + L^{-T}*u | ||u||_2 = 1}
Sigma = matrix([1.0, 0.0, 0.0, 1.0], (2,2))
bnd, P, q, r, X = cheb(A0, b0, Sigma)
xc = -q
L = +P
lapack.posv(L, xc)
L /= sqrt(1 - r - blas.dot(q, xc))
if pylab_installed:
def makefig1():
pylab.figure(1, facecolor='w', figsize=(6,6))
pylab.plot(V[0,:].T, V[1,:].T, 'b-')
nopts = 1000
angles = matrix( [a*2.0*pi/nopts for a in range(nopts) ],
(1,nopts) )
circle = matrix(0.0, (2,nopts))
circle[0,:], circle[1,:] = cos(angles), sin(angles)
for k in range(len(C)):
c = C[k]
pylab.plot([c[0]], [c[1]], 'ow')
pylab.text(c[0], c[1], "s%d" %k)
pylab.plot(c[0] + circle[0,:].T, c[1]+circle[1,:].T, 'g:')
if k >= 1:
v = V[:,k-1]
if k==1:
dir = 0.5 * (C[k] + C[-1]) - v
else:
dir = 0.5 * (C[k] + C[k-1]) - v
pylab.plot([v[0], v[0] + 5*dir[0]],
[v[1], v[1] + 5*dir[1]], 'b-')
ellipse = +circle
blas.trsm(L, ellipse, transA='T')
pylab.plot(xc[0] + ellipse[0,:].T, xc[1]+ellipse[1,:].T, 'r-')
for Xk in X:
pylab.plot([Xk[0]], [Xk[1]], 'ro')
pylab.axis([-5, 5, -5, 5])
pylab.title('Geometrical interpretation of Chebyshev bound (fig. 7.7)')
pylab.axis('off')
makefig1()
#print("Close figure to continue.")
#pylab.show()
# Compute bounds for s0 with sigma in [0,2.5]
nosigmas = 150
sigmas = 0.001 + (2.5 - 0.001) / nosigmas * matrix(list(range(nosigmas)),
tc='d')
I = matrix([1.0, 0.0, 0.0, 1.0], (2,2))
print("Computing lower bounds for symbol 0 ...")
bnds0 = [ cheb(A0, b0, sigma**2*I)[0] for sigma in sigmas ]
if pylab_installed:
pylab.figure(2,facecolor='w')
pylab.plot(sigmas, bnds0)
pylab.axis([0, 2.5, 0.0, 1.0])
pylab.title('Chebyshev lower bounds (fig 7.6)')
pylab.text(sigmas[nosigmas/2], bnds0[nosigmas/2], 's0')
pylab.xlabel('sigma')
pylab.ylabel('Probability of correct detection')
#print("Close figure to continue.")
#pylab.show()
# Bounds for s1.
b1 -= A1*C[1] # put s1 at the origin
print("Computing lower bounds for symbol 1 ...")
bnds1 = [ cheb(A1, b1, sigma**2*I)[0] for sigma in sigmas ]
if pylab_installed:
pylab.figure(2,facecolor='w')
pylab.plot(sigmas,bnds0, '-b', sigmas, bnds1, 'r')
pylab.axis([0, 2.5, 0.0, 1.0])
pylab.title('Chebyshev lower bounds (fig 7.6)')
pylab.text(sigmas[nosigmas/2], bnds0[nosigmas/2], 's0')
pylab.text(sigmas[nosigmas/2], bnds1[nosigmas/2], 's1')
pylab.xlabel('sigma')
pylab.ylabel('Probability of correct detection')
#print("Close figure to continue.")
#pylab.show()
# Bounds for s2.
b2 -= A2*C[2] # put s2 at the origin
print("Computing lower bounds for symbol 2 ...")
bnds2 = [ cheb(A2, b2, sigma**2*I)[0] for sigma in sigmas ]
if pylab_installed:
makefig1()
pylab.figure(2,facecolor='w')
pylab.plot(sigmas,bnds0, '-b', sigmas, bnds1, 'r', sigmas, bnds2, 'g')
pylab.axis([0, 2.5, 0.0, 1.0])
pylab.title('Chebyshev lower bounds (fig 7.6)')
pylab.text(sigmas[nosigmas/2], bnds0[nosigmas/2], 's0')
pylab.text(sigmas[nosigmas/2], bnds1[nosigmas/2], 's1')
pylab.text(sigmas[nosigmas/2], bnds2[nosigmas/2], 's2')
pylab.xlabel('sigma')
pylab.ylabel('Probability of correct detection')
pylab.show()