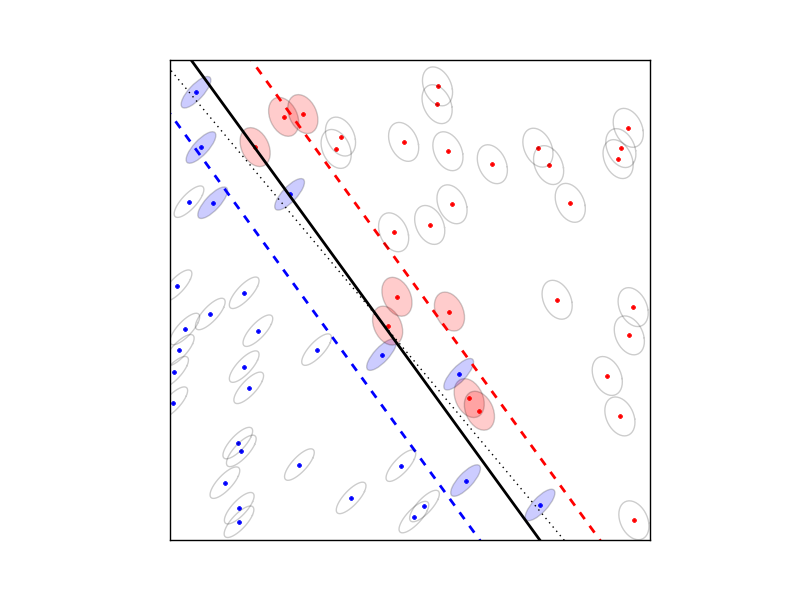
Robust SVM
The robust SVM training problem can be expressed as a cone QP with second-order cone constraints:
The variables are \(w \in \mathbf{R}^n\), \(b \in \mathbf{R}\), \(v \in \mathbf{R}^N\), and \(u \in \mathbf{R}^t\). The matrix \(X \in \mathbf{R}^{N\times n}\) has as its rows the training examples \(x_i^T\) and the vector \(d \in \{-1, 1\}^N\) contains the training labels. The matrices \(S_j\) define the shape and the size of the uncertainty ellipsoids, and the matrix \(E\) is a selector matrix with zeros and one ‘1’ per row. \(E_{ij} = 1\) means that the i’th training vector is associated with the j’th uncertainty ellipsoid. For \(t = 0\), the term \(Eu\) and the norm constraints are absent, and the problem reduces to the standard linear SVM
Documentation
A custom solver for the robust SVM problem is available as a Python
module robsvm.py. The module implements the following function:
- robsvm(X, labels, gamma, P, e)
Solves the ‘soft-margin’ robust SVM problem.
The first three input arguments are the data matrix \(X\) (with the \(N\) training examples \(x_i^T\) as rows), the label vector \(d\), and the positive parameter \(\gamma\). The fourth input argument P must be a Python list of \(t\) matrices \(S_1,\ldots,S_t\). The last argument e is an \(N\)-vector where the i’th element \(e_i \in \{0,..,t-1\}\) is the index of the uncertainty ellipsoid associated with the i’th training vector.
The function returns \(w\), \(b\), \(u\), \(v\), and the number of iterations (an integer).
Example
from robsvm import robsvm
from cvxopt import matrix, normal, uniform
# parameters
m, n = 60, 2
gamma = 10.0
# generate random problem data
X = 2.0*uniform(m,n)-1.0
d = matrix(1,(m,1))
# generate noisy labels
w0 = matrix([2.0,1.0])+normal(2,1); b0 = 0.4
z = 0.2*normal(m,1)
for i in range(m):
if (X[i,:]*w0)[0] + b0 < z[i]: d[i] = -1
# generate uncertainty ellipsoids
k = 2
P = [0.1*normal(4*n,n) for i in range(k)]
P = [ p.T*p for p in P]
e = matrix(0,(m,1))
for i in xrange(m):
if d[i] == -1: e[i] = 1
# solve SVM training problem
w, b, u, v, iterations = robsvm(X, d, gamma, P, e)