# Figures 8.5-7, pages 417-421.
# Centers of polyhedra.
from math import log, pi
from cvxopt import blas, lapack, solvers
from cvxopt import matrix, spdiag, sqrt, mul, cos, sin, log
from cvxopt.modeling import variable, op
solvers.options['show_progress'] = False
try: import pylab
except ImportError: pylab_installed = False
else: pylab_installed = True
# Extreme points (with first one appended at the end)
X = matrix([ 0.55, 0.25, -0.20, -0.25, 0.00, 0.40, 0.55,
0.00, 0.35, 0.20, -0.10, -0.30, -0.20, 0.00 ], (7,2))
m = X.size[0] - 1
# Inequality description G*x <= h with h = 1
G, h = matrix(0.0, (m,2)), matrix(0.0, (m,1))
G = (X[:m,:] - X[1:,:]) * matrix([0., -1., 1., 0.], (2,2))
h = (G * X.T)[::m+1]
G = mul(h[:,[0,0]]**-1, G)
h = matrix(1.0, (m,1))
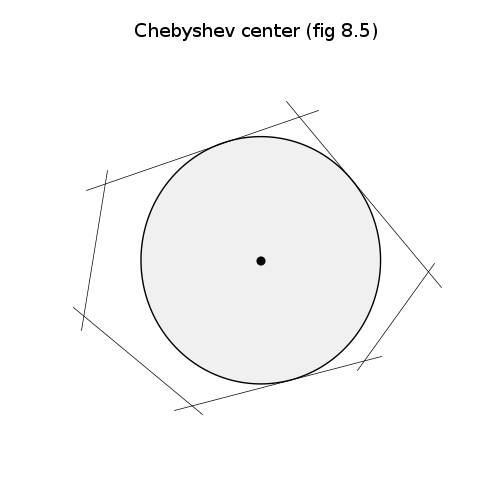
# Chebyshev center
#
# maximizse R
# subject to gk'*xc + R*||gk||_2 <= hk, k=1,...,m
# R >= 0
R = variable()
xc = variable(2)
op(-R, [ G[k,:]*xc + R*blas.nrm2(G[k,:]) <= h[k] for k in range(m) ] +
[ R >= 0] ).solve()
R = R.value
xc = xc.value
if pylab_installed:
pylab.figure(1, facecolor='w')
# polyhedron
for k in range(m):
edge = X[[k,k+1],:] + 0.1 * matrix([1., 0., 0., -1.], (2,2)) * \
(X[2*[k],:] - X[2*[k+1],:])
pylab.plot(edge[:,0], edge[:,1], 'k')
# 1000 points on the unit circle
nopts = 1000
angles = matrix( [ a*2.0*pi/nopts for a in range(nopts) ], (1,nopts) )
circle = matrix(0.0, (2,nopts))
circle[0,:], circle[1,:] = R*cos(angles), R*sin(angles)
circle += xc[:,nopts*[0]]
# plot maximum inscribed disk
pylab.fill(circle[0,:].T, circle[1,:].T, facecolor = '#F0F0F0')
pylab.plot([xc[0]], [xc[1]], 'ko')
pylab.title('Chebyshev center (fig 8.5)')
pylab.axis('equal')
pylab.axis('off')
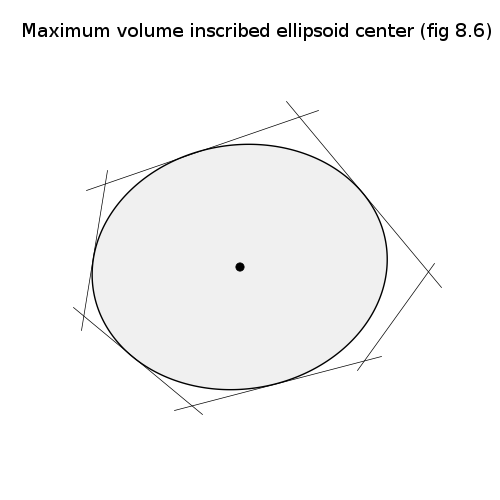
# Maximum volume enclosed ellipsoid center
#
# minimize -log det B
# subject to ||B * gk||_2 + gk'*c <= hk, k=1,...,m
#
# with variables B and c.
#
# minimize -log det L
# subject to ||L' * gk||_2^2 / (hk - gk'*c) <= hk - gk'*c, k=1,...,m
#
# L lower triangular with positive diagonal and B*B = L*L'.
#
# minimize -log x[0] - log x[2]
# subject to g( Dk*x + dk ) <= 0, k=1,...,m
#
# g(u,t) = u'*u/t - t
# Dk = [ G[k,0] G[k,1] 0 0 0
# 0 0 G[k,1] 0 0
# 0 0 0 -G[k,0] -G[k,1] ]
# dk = [0; 0; h[k]]
#
# 5 variables x = (L[0,0], L[1,0], L[1,1], c[0], c[1])
D = [ matrix(0.0, (3,5)) for k in range(m) ]
for k in range(m):
D[k][ [0, 3, 7, 11, 14] ] = matrix( [G[k,0], G[k,1], G[k,1],
-G[k,0], -G[k,1]] )
d = [matrix([0.0, 0.0, hk]) for hk in h]
def F(x=None, z=None):
if x is None:
return m, matrix([ 1.0, 0.0, 1.0, 0.0, 0.0 ])
if min(x[0], x[2], min(h-G*x[3:])) <= 0.0:
return None
y = [ Dk*x + dk for Dk, dk in zip(D, d) ]
f = matrix(0.0, (m+1,1))
f[0] = -log(x[0]) - log(x[2])
for k in range(m):
f[k+1] = y[k][:2].T * y[k][:2] / y[k][2] - y[k][2]
Df = matrix(0.0, (m+1,5))
Df[0,0], Df[0,2] = -1.0/x[0], -1.0/x[2]
# gradient of g is ( 2.0*(u/t); -(u/t)'*(u/t) -1)
for k in range(m):
a = y[k][:2] / y[k][2]
gradg = matrix(0.0, (3,1))
gradg[:2], gradg[2] = 2.0 * a, -a.T*a - 1
Df[k+1,:] = gradg.T * D[k]
if z is None: return f, Df
H = matrix(0.0, (5,5))
H[0,0] = z[0] / x[0]**2
H[2,2] = z[0] / x[2]**2
# Hessian of g is (2.0/t) * [ I, -u/t; -(u/t)', (u/t)*(u/t)' ]
for k in range(m):
a = y[k][:2] / y[k][2]
hessg = matrix(0.0, (3,3))
hessg[0,0], hessg[1,1] = 1.0, 1.0
hessg[:2,2], hessg[2,:2] = -a, -a.T
hessg[2, 2] = a.T*a
H += (z[k] * 2.0 / y[k][2]) * D[k].T * hessg * D[k]
return f, Df, H
sol = solvers.cp(F)
L = matrix([sol['x'][0], sol['x'][1], 0.0, sol['x'][2]], (2,2))
c = matrix([sol['x'][3], sol['x'][4]])
if pylab_installed:
pylab.figure(2, facecolor='w')
# polyhedron
for k in range(m):
edge = X[[k,k+1],:] + 0.1 * matrix([1., 0., 0., -1.], (2,2)) * \
(X[2*[k],:] - X[2*[k+1],:])
pylab.plot(edge[:,0], edge[:,1], 'k')
# 1000 points on the unit circle
nopts = 1000
angles = matrix( [ a*2.0*pi/nopts for a in range(nopts) ], (1,nopts) )
circle = matrix(0.0, (2,nopts))
circle[0,:], circle[1,:] = cos(angles), sin(angles)
# ellipse = L * circle + c
ellipse = L * circle + c[:, nopts*[0]]
pylab.fill(ellipse[0,:].T, ellipse[1,:].T, facecolor = '#F0F0F0')
pylab.plot([c[0]], [c[1]], 'ko')
pylab.title('Maximum volume inscribed ellipsoid center (fig 8.6)')
pylab.axis('equal')
pylab.axis('off')
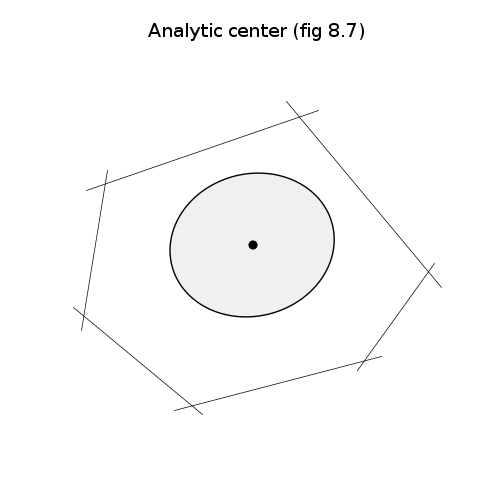
# Analytic center.
#
# minimize -sum log (h-G*x)
#
def F(x=None, z=None):
if x is None: return 0, matrix(0.0, (2,1))
y = h-G*x
if min(y) <= 0: return None
f = -sum(log(y))
Df = (y**-1).T * G
if z is None: return matrix(f), Df
H = G.T * spdiag(y**-2) * G
return matrix(f), Df, z[0]*H
sol = solvers.cp(F)
xac = sol['x']
Hac = G.T * spdiag((h-G*xac)**-1) * G
if pylab_installed:
pylab.figure(3, facecolor='w')
# polyhedron
for k in range(m):
edge = X[[k,k+1],:] + 0.1 * matrix([1., 0., 0., -1.], (2,2)) * \
(X[2*[k],:] - X[2*[k+1],:])
pylab.plot(edge[:,0], edge[:,1], 'k')
# 1000 points on the unit circle
nopts = 1000
angles = matrix( [ a*2.0*pi/nopts for a in range(nopts) ], (1,nopts) )
circle = matrix(0.0, (2,nopts))
circle[0,:], circle[1,:] = cos(angles), sin(angles)
# ellipse = L^-T * circle + xc where Hac = L*L'
lapack.potrf(Hac)
ellipse = +circle
blas.trsm(Hac, ellipse, transA='T')
ellipse += xac[:, nopts*[0]]
pylab.fill(ellipse[0,:].T, ellipse[1,:].T, facecolor = '#F0F0F0')
pylab.plot([xac[0]], [xac[1]], 'ko')
pylab.title('Analytic center (fig 8.7)')
pylab.axis('equal')
pylab.axis('off')
pylab.show()