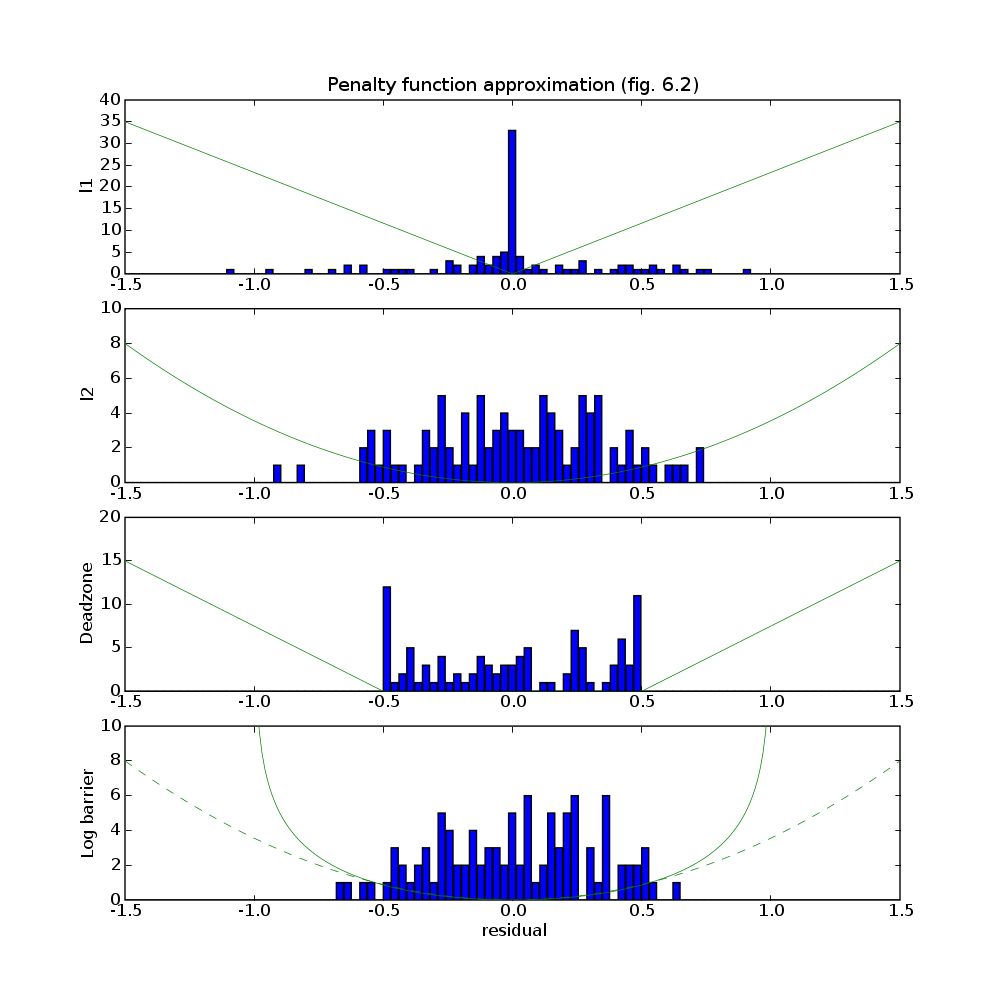
# Figure 6.2, page 297.
# Penalty approximation.
#
# The problem data are not the same as in the book figure.
from cvxopt import lapack, solvers, matrix, spdiag, log, div, normal
from cvxopt.modeling import variable, op, max, sum
solvers.options['show_progress'] = 0
try: import numpy, pylab
except ImportError: pylab_installed = False
else: pylab_installed = True
m, n = 100, 30
A = normal(m,n)
b = normal(m,1)
b /= (1.1 * max(abs(b))) # Make x = 0 feasible for log barrier.
# l1 approximation
#
# minimize || A*x + b ||_1
x = variable(n)
op(sum(abs(A*x+b))).solve()
x1 = x.value
if pylab_installed:
pylab.figure(1, facecolor='w', figsize=(10,10))
pylab.subplot(411)
nbins = 100
bins = [-1.5 + 3.0/(nbins-1)*k for k in range(nbins)]
pylab.hist( A*x1+b , numpy.array(bins))
nopts = 200
xs = -1.5 + 3.0/(nopts-1) * matrix(list(range(nopts)))
pylab.plot(xs, (35.0/1.5) * abs(xs), 'g-')
pylab.axis([-1.5, 1.5, 0, 40])
pylab.ylabel('l1')
pylab.title('Penalty function approximation (fig. 6.2)')
# l2 approximation
#
# minimize || A*x + b ||_2
x = matrix(0.0, (m,1))
lapack.gels(+A, x)
x2 = x[:n]
if pylab_installed:
pylab.subplot(412)
pylab.hist(A*x2+b, numpy.array(bins))
pylab.plot(xs, (8.0/1.5**2) * xs**2 , 'g-')
pylab.ylabel('l2')
pylab.axis([-1.5, 1.5, 0, 10])
# Deadzone approximation
#
# minimize sum(max(abs(A*x+b)-0.5, 0.0))
x = variable(n)
op(sum(max(abs(A*x+b)-0.5, 0.0))).solve()
xdz = x.value
if pylab_installed:
pylab.subplot(413)
pylab.hist(A*xdz+b, numpy.array(bins))
pylab.plot(xs, 15.0/1.0 * matrix([ max(abs(xk)-0.5, 0.0) for xk
in xs ]), 'g-')
pylab.ylabel('Deadzone')
pylab.axis([-1.5, 1.5, 0, 20])
# Log barrier
#
# minimize -sum (log ( 1.0 - A*x+b)**2)
def F(x=None, z=None):
if x is None: return 0, matrix(0.0, (n,1))
y = A*x+b
if max(abs(y)) >= 1.0: return None
f = -sum(log(1.0 - y**2))
gradf = 2.0 * A.T * div(y, 1-y**2)
if z is None: return f, gradf.T
H = A.T * spdiag(2.0 * z[0] * div( 1.0+y**2, (1.0 - y**2)**2 )) * A
return f, gradf.T, H
xlb = solvers.cp(F)['x']
if pylab_installed:
pylab.subplot(414)
pylab.hist(A*xlb+b, numpy.array(bins))
nopts = 200
pylab.plot(xs, (8.0/1.5**2) * xs**2, 'g--')
xs2 = -0.99999 + (2*0.99999 /(nopts-1)) * matrix(list(range(nopts)))
pylab.plot(xs2, -3.0 * log(1.0 - abs(xs2)**2), 'g-')
pylab.ylabel('Log barrier')
pylab.xlabel('residual')
pylab.axis([-1.5, 1.5, 0, 10])
pylab.show()