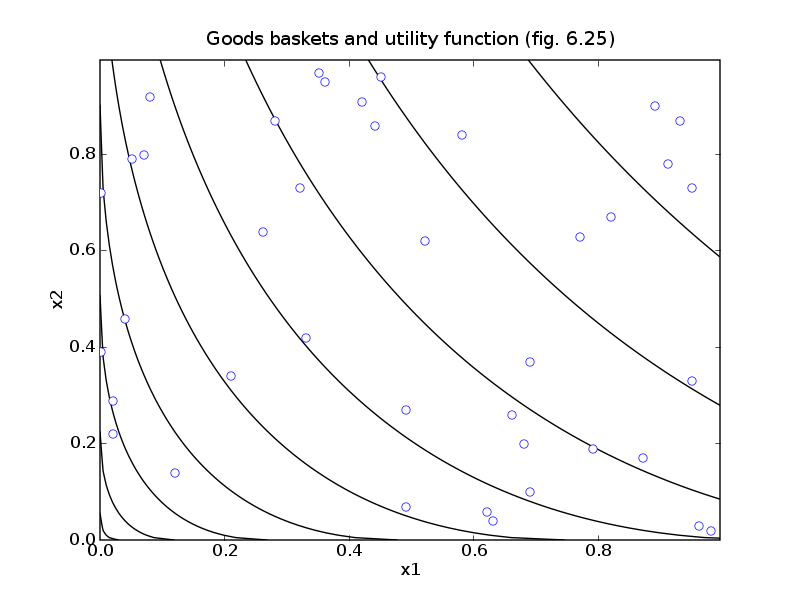
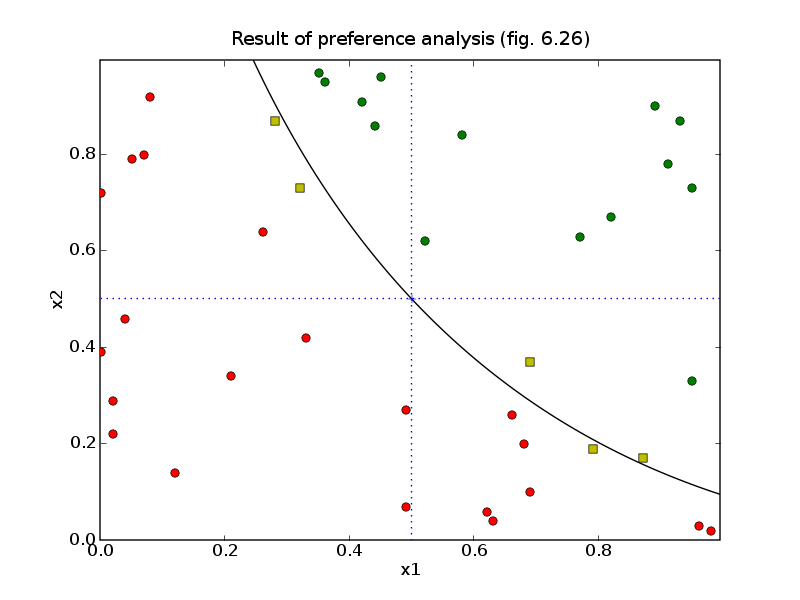
# Figures 6.25 and 6.26, page 342.
# Consumer preference analysis.
from cvxopt import solvers, matrix, sqrt
from cvxopt.modeling import variable, op
solvers.options['show_progress'] = 0
try: import pylab
except ImportError: pylab_installed = False
else: pylab_installed = True
def utility(x, y):
return (1.1 * sqrt(x) + 0.8 * sqrt(y)) / 1.9
B = matrix([
4.5e-01, 9.6e-01,
2.1e-01, 3.4e-01,
2.8e-01, 8.7e-01,
9.6e-01, 3.0e-02,
8.0e-02, 9.2e-01,
2.0e-02, 2.2e-01,
0.0e+00, 3.9e-01,
2.6e-01, 6.4e-01,
3.5e-01, 9.7e-01,
9.1e-01, 7.8e-01,
1.2e-01, 1.4e-01,
5.8e-01, 8.4e-01,
3.2e-01, 7.3e-01,
4.9e-01, 2.7e-01,
7.0e-02, 8.0e-01,
9.3e-01, 8.7e-01,
4.4e-01, 8.6e-01,
3.3e-01, 4.2e-01,
8.9e-01, 9.0e-01,
4.9e-01, 7.0e-02,
9.5e-01, 3.3e-01,
6.6e-01, 2.6e-01,
9.5e-01, 7.3e-01,
4.2e-01, 9.1e-01,
6.8e-01, 2.0e-01,
8.7e-01, 1.7e-01,
5.2e-01, 6.2e-01,
7.7e-01, 6.3e-01,
2.0e-02, 2.9e-01,
9.8e-01, 2.0e-02,
5.0e-02, 7.9e-01,
7.9e-01, 1.9e-01,
6.2e-01, 6.0e-02,
6.9e-01, 1.0e-01,
6.9e-01, 3.7e-01,
0.0e+00, 7.2e-01,
6.3e-01, 4.0e-02,
4.0e-02, 4.6e-01,
3.6e-01, 9.5e-01,
8.2e-01, 6.7e-01 ], (2, 40))
m = B.size[1]
# Plot some contour lines.
nopts = 200
a = (1.0/nopts)*matrix(range(nopts), tc='d')
X, Y = a[:,nopts*[0]].T, a[:,nopts*[0]]
if pylab_installed:
pylab.figure(1, facecolor='w')
pylab.plot(B[0,:], B[1,:], 'wo', markeredgecolor='b')
pylab.contour(pylab.array(X), pylab.array(Y), pylab.array(utility(X,Y)),
[.1*(k+1) for k in range(9)], colors='k')
pylab.xlabel('x1')
pylab.ylabel('x2')
pylab.title('Goods baskets and utility function (fig. 6.25)')
#print("Close figure to start analysis.")
#pylab.show()
# P are basket indices in order of increasing preference
l = list(zip(utility(B[0,:], B[1,:]), range(m)))
l.sort()
P = [ e[1] for e in l ]
# baskets with known preference relations
u = variable(m)
gx = variable(m)
gy = variable(m)
# comparison basket at (.5, .5) has utility 0
gxc = variable(1)
gyc = variable(1)
monotonicity = [ gx >= 0, gy >= 0, gxc >= 0, gyc >= 0 ]
preferences = [ u[P[j+1]] >= u[P[j]] + 1.0 for j in range(m-1) ]
concavity = [ u[j] <= u[i] + gx[i] * ( B[0,j] - B[0,i] ) +
gy[i] * ( B[1,j] - B[1,i] ) for i in range(m) for j in range(m) ]
concavity += [ 0 <= u[i] + gx[i] * ( 0.5 - B[0,i] ) +
gy[i] * ( 0.5 - B[1,i] ) for i in range(m) ]
concavity += [ u[j] <= gxc * ( B[0,j] - 0.5 ) +
gyc * ( B[1,j] - 0.5 ) for j in range(m) ]
preferred, rejected, neutral = [], [], []
for k in range(m):
p = op(-u[k], monotonicity + preferences + concavity)
p.solve()
if p.status == 'optimal' and p.objective.value()[0] > 0:
rejected += [k]
print("Basket (%1.2f, %1.2f) rejected." %(B[0,k],B[1,k]))
else:
p = op(u[k], monotonicity + preferences + concavity)
p.solve()
if p.status == 'optimal' and p.objective.value()[0] > 0:
print("Basket (%1.2f, %1.2f) preferred." %(B[0,k],B[1,k]))
preferred += [k]
else:
print("No conclusion about basket (%1.2f, %1.2f)." \
%(B[0,k],B[1,k]))
neutral += [k]
if pylab_installed:
pylab.figure(1, facecolor='w')
pylab.plot(B[0,:], B[1,:], 'wo', markeredgecolor='b')
pylab.contour(pylab.array(X), pylab.array(Y), pylab.array(utility(X,Y)),
[.1*(k+1) for k in range(9)], colors='k')
pylab.xlabel('x1')
pylab.ylabel('x2')
pylab.title('Goods baskets and utility function (fig. 6.25)')
pylab.figure(2, facecolor='w')
pylab.plot(B[0,preferred], B[1,preferred], 'go')
pylab.plot(B[0,rejected], B[1,rejected], 'ro')
pylab.plot(B[0,neutral], B[1,neutral], 'ys')
pylab.plot([0.5], [0.5], '+')
pylab.plot([0.5, 0.5], [0,1], ':', [0,1], [0.5,0.5], ':')
pylab.axis([0,1,0,1])
pylab.contour(pylab.array(X), pylab.array(Y), pylab.array(utility(X,Y)),
[utility(0.5,0.5)], colors='k')
pylab.xlabel('x1')
pylab.ylabel('x2')
pylab.title('Result of preference analysis (fig. 6.26)')
pylab.show()